Heptagonálne Prism funkcie a ako vypočítať objem
heptagonálny hranol je geometrický obrazec, ktorý, ako už názov napovedá, zahŕňa dve geometrické definície, ktorými sú: hranol a heptagon.
"Hranol" je geometrický útvar obmedzený dvoma základňami, ktoré sú rovné a rovnobežné polygóny a ich bočné plochy sú rovnobežníky.
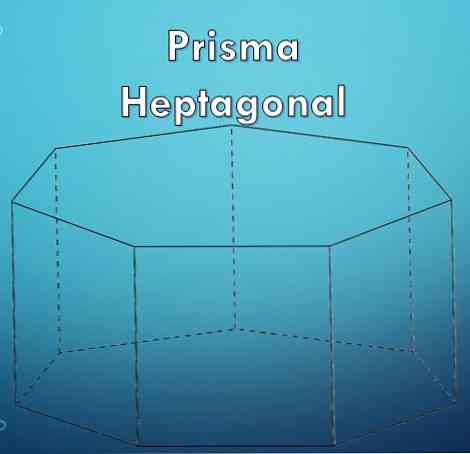
"Heptagon" je polygón, ktorý je tvorený siedmimi (7) stranami. Pretože heptagon je polygón, môže to byť pravidelné alebo nepravidelné.
O polygóne sa hovorí, že je pravidelný, ak všetky jeho strany majú rovnakú dĺžku a ich vnútorné uhly sú rovnaké, nazývajú sa tiež rovnostranné polygóny; inak sa hovorí, že mnohouholník je nepravidelný.

Charakteristiky hepatálneho prizmu
Nasledujú určité vlastnosti, ktoré majú heptagonálny hranol, ako sú: jeho konštrukcia, vlastnosti jeho základov, plocha všetkých jeho tvárí a jej objem.
1. Stavba
Na konštrukciu heponomálneho hranolu sú potrebné dva heptagóny, ktoré budú jeho bázami a siedmimi paralelogrammi, jeden na každej strane heptagonu..
Začnite tým, že kreslí heptagon, potom nakreslite sedem zvislých čiar rovnakej dĺžky, ktoré pochádzajú z každého z jeho vrcholov.
Nakoniec sa nakreslí ďalší heptagon, takže jeho vrcholy sa zhodujú s koncami čiar nakreslených v predchádzajúcom kroku.
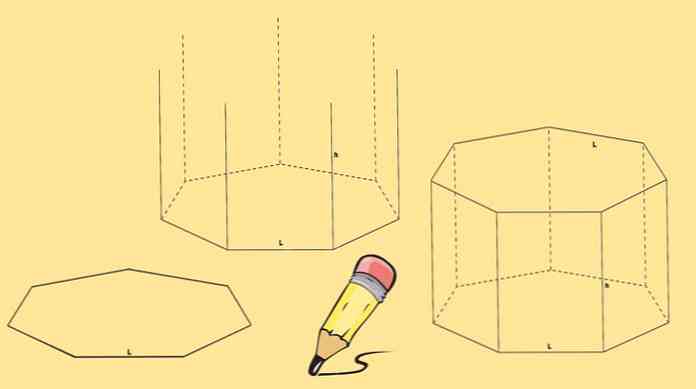
Heptagonálny hranol uvedený vyššie sa nazýva priamy heptagonálny hranol. Ale môžete mať aj šikmý heptagonálny hranol ako ten na nasledujúcom obrázku.

2- Vlastnosti jeho báz
Pretože ich bázy sú heptagóny, sú v súlade s tým, že diagonálne číslo je D = nx (n-3) / 2, kde "n" je počet strán polygónu; v tomto prípade máme D = 7 × 4/2 = 14.
Môžeme tiež vidieť, že súčet vnútorných uhlov akéhokoľvek heptagonu (pravidelného alebo nepravidelného) je rovný 900º. Toto môže byť overené nasledujúcim obrázkom.
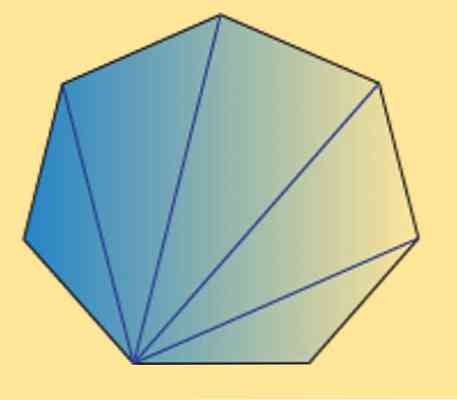
Ako vidíte, existuje 5 vnútorných trojuholníkov a pomocou súčtu vnútorných uhlov trojuholníka sa rovná 180 °, možno dosiahnuť, že požadovaný výsledok.
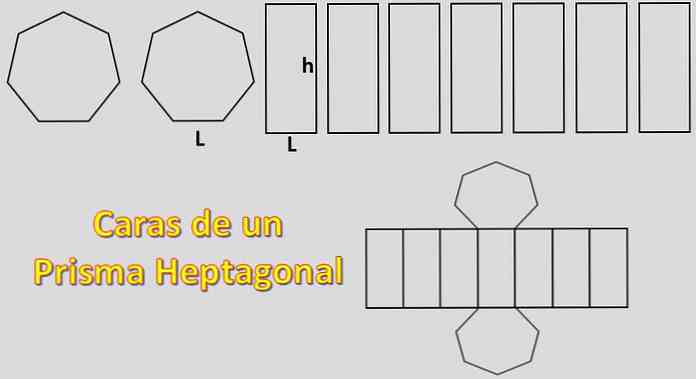
3 - Plocha potrebná na vytvorenie Heptagonálneho Prizmu
Pretože jeho bázy sú dva heptagóny a jeho strany sú sedem paralelogramov, plocha potrebná na vytvorenie heptagonálneho hranolu je rovná 2xH + 7xP, kde "H" je plocha každého heptagonu a "P" plocha každého rovnobežníka.
V tomto prípade sa vypočíta plocha pravidelného heptagonu. Preto je dôležité poznať definíciu apotémy.
Apothem je kolmá čiara, ktorá prechádza od stredu pravidelného mnohouholníka do stredu ktorejkoľvek jeho strany..
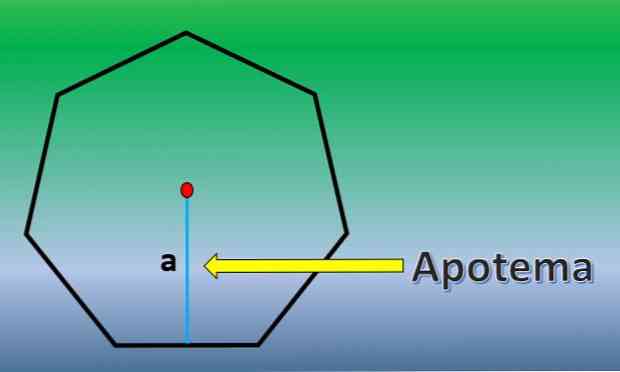
Akonáhle je známy apotém, oblasť heptagonu je H = 7xLxa / 2, kde "L" je dĺžka každej strany a "a" dĺžka apotému..
Plocha rovnobežníka sa dá ľahko vypočítať, je definovaná ako P = Lxh, kde "L" je rovnaká dĺžka strany heptagonu a "h" je výška hranolu.
Na záver, množstvo materiálu potrebného na vytvorenie heptagonálneho hranolu (s pravidelnými bázami) je 7xLxa + 7xLxh, tj 7xL (a + h).
4- Hlasitosť
Keď je známa plocha základne a výška hranolu, objem je definovaný ako (základná plocha) x (výška).
V prípade heponomálneho hranolu (s pravidelnou bázou) má objem V = 7xLxaxh / 2; môže byť tiež zapísaný ako V = Pxaxh / 2, kde "P" je obvod pravidelného heptagonu.
referencie
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: prístup k riešeniu problémov učiteľov základných škôl. López Mateos Editori.
- Fregoso, R. S., & Carrera, S.A. (2005). Matematika 3. Editorial Progreso.
- Gallardo, G., & Pilar, P. M. (2005). Matematika 6. Editorial Progreso.
- Gutiérrez, C. T., & Cisneros, M. P. (2005). 3. Matematický kurz. Editorial Progreso.
- Kinsey, L., & Moore, T. E. (2006). Symetria, tvar a priestor: Úvod do matematiky prostredníctvom geometrie (ilustrovaný, dotlač ed.). Springer Science & Business Media.
- Mitchell, C. (1999). Oslňujúci Matematika Line vzory (Ilustrated ed.). Scholastic Inc.
- R., M. P. (2005). Kreslím 6º. Editorial Progreso.


