Koľko hrany má hexagonálny hranol?

Vedieť koľko hrán má hexagonálny hranol musí byť známy význam "hrany", "hranol" a "hexagonálny". Prvé dva pojmy sú všeobecné definície a tretí pojem súvisí s tvarom geometrického útvaru.

Keď hovoríme o šesťuholníku, spomína sa šesťuholník. Predpona "hexa" znamená, že mnohouholník má šesť strán.

Okraj je okrajom objektu. Geometricky je to čiara, ktorá spája dva po sebe idúce vrcholy geometrického útvaru.

Hranol je geometrická postava obmedzená dvoma základňami, ktoré sú rovnobežné a rovné polygóny a ich bočné plochy sú rovnobežníky.

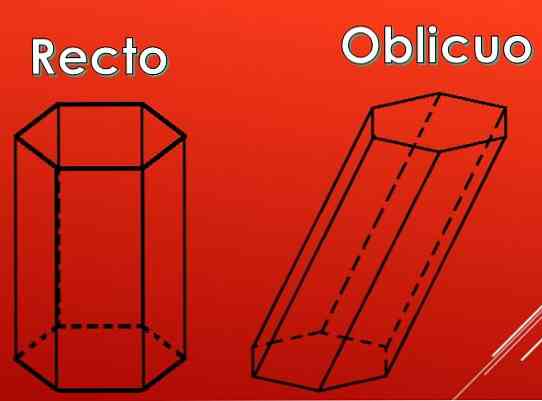
Na nasledujúcom obrázku je možné vidieť, že bočné plochy hexagonálneho hranolu môžu byť obdĺžniky, ale môžu to byť aj paralelogramy..

Podľa typu paralelogramov je možné poistné rozdeliť do dvoch typov: rovné a šikmé.

Ako spočítať hrany hexagonálneho hranolu?

Počet hrán, ktoré bude mať hexagonálny hranol, sa nezmení, ak sa jedná o rovný alebo šikmý hranol. Tiež počet hrán nezávisí od dĺžky strán.

Počítanie okrajov hexagonálneho hranolu sa môže uskutočniť niekoľkými spôsobmi. Tu sú dva spôsoby:

1. Rozložte hranol

Jedným zo spôsobov, ako spočítať hrany, je rozklad hexagonálneho hranolu v jeho dvoch základniach a jeho bočných plochách. Týmto spôsobom získate dva šesťuholníky a paralelogram s piatimi vnútornými čiarami.

Každý šesťuholník má šesť hrán, preto hranol bude mať viac ako 12 hrán.

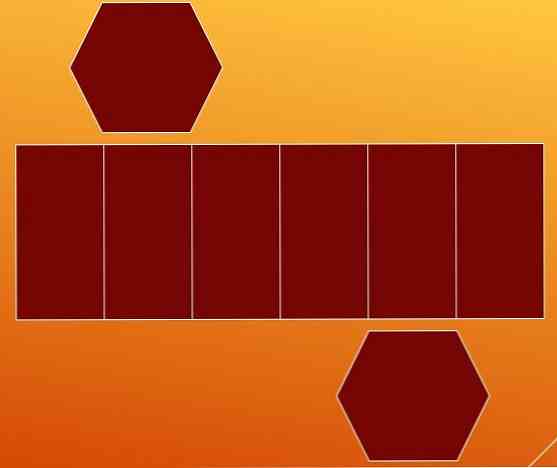
Na prvý pohľad sa predpokladá, že rovnobežník obsahuje deväť hrán (sedem zvislých a dve vodorovné). Ale je vhodné zastaviť analýzu tohto prípadu.

Keď je rovnobežník ohnutý, aby vytvoril hranol, je vidieť, že prvý riadok vľavo sa spojí s posledným riadkom vpravo, s ktorým obe čiary predstavujú jeden okraj..

Ale čo tie dve horizontálne čiary?

Keď sú všetky kusy znovu spojené, horizontálne čiary budú spojené, každá so šiestimi hranami každého šesťuholníka. Z tohto dôvodu by bolo ich počítanie samostatne.

Takže rovnobežník obsahuje šesť hrán hranola, ktoré spolu s 12 hranami počítanými na začiatku dáva celkom 18 hrán.

2.- Premietanie každej hrany

Ďalším spôsobom, veľa jednoduchšie počítať hrany, je použitie skutočnosti, že základne šesťhranných hranolov sú šesťuholníky, potom každá základňa má šesť hrán.

Na druhej strane, z každého vrcholu šesťuholníka sa premieta jedna hrana na zodpovedajúci vrchol druhého šesťuholníka; to znamená, že existuje šesť hrán, ktoré spájajú jednu základňu s druhou.

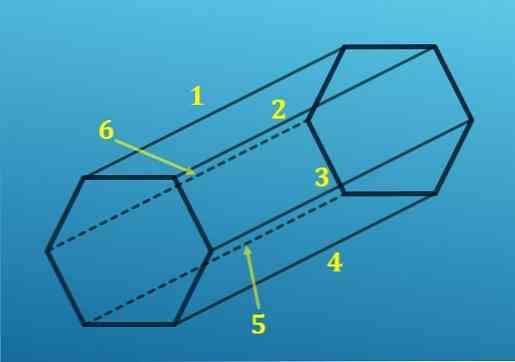
Pridaním všetkých hrán získate celkom 18 hrán.

záver

Je možné preukázať, že počet hraníc hranolu sa rovná trojnásobku počtu hrán, ktoré má polygón, ktorý ho tvorí..

Preto päťuholníkový hranol bude mať 3 * 5 = 15 hrán, heptagonálny hranol bude mať 3 * 7 = 21 hrán a môže byť teda aplikovaný na akýkoľvek hranol.

referencie

1. Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: prístup k riešeniu problémov učiteľov základných škôl. López Mateos Editori.
2. Fregoso, R. S., & Carrera, S.A. (2005). Matematika 3. Editorial Progreso.
3. Gallardo, G., & Pilar, P. M. (2005). Matematika 6. Editorial Progreso.
4. Gutiérrez, C. T., & Cisneros, M. P. (2005). 3. Matematický kurz. Editorial Progreso.
5. Kinsey, L., & Moore, T. E. (2006). Symetria, tvar a priestor: Úvod do matematiky prostredníctvom geometrie (ilustrovaný, dotlač ed.). Springer Science & Business Media.
6. Mitchell, C. (1999). Oslňujúci Matematika Line vzory (Ilustrated ed.). Scholastic Inc.
7. R., M. P. (2005). Kreslím 6º. Editorial Progreso.