Vlastnosti kapilárnosti a príklad vo vode
kapilarita Je to vlastnosť kvapalín, ktorá im umožňuje pohyb cez rúrkové otvory alebo porézne povrchy aj proti gravitačnej sile. Na tento účel musí existovať rovnováha a koordinácia dvoch síl súvisiacich s molekulami kvapaliny: súdržnosť a adhézia; ktoré majú tieto dva fyzikálne odrazy nazývané povrchové napätie.
Kvapalina musí byť schopná zvlhčiť vnútorné steny rúrky alebo póry materiálu, ktorým sa pohybuje. K tomu dochádza, keď je adhézna sila (stena kapilárnej trubice) väčšia ako medzimolekulová kohézna sila. V dôsledku toho kvapalné molekuly vytvárajú silnejšie interakcie s atómami materiálu (sklo, papier atď.) Ako medzi nimi.
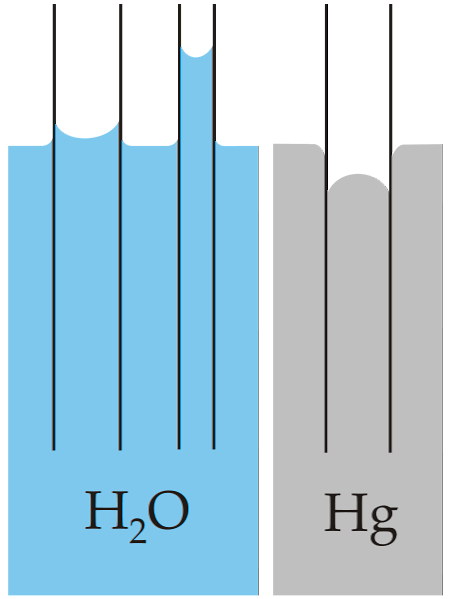
Klasický príklad kapilárnosti je znázornený v porovnaní tejto vlastnosti pre dve veľmi odlišné kvapaliny: vodu a ortuť.
Horný obrázok ukazuje, že voda stúpa cez steny rúrky, čo znamená, že má vyššie adhézne sily; zatiaľ čo opak sa deje s ortuťou, pretože jej kohézne, kovové spojovacie sily zabraňujú zmáčaniu skla.
Z tohto dôvodu voda vytvára konkávny meniskus a ortuť je konvexný meniskus (kupolovitý). Treba tiež poznamenať, že čím menší je polomer rúry alebo úsek, cez ktorý sa kvapalina pohybuje, tým väčšia je prejdená výška alebo vzdialenosť (porovnaj výšky vodných stĺpcov pre obe rúry)..
index
- 1 Charakteristika kapilárnosti
- 1.1 - Povrch kvapaliny
- 1.2 -Hmotnosť
- 1.3 - Povrchové napätie
- 1.4 -Radio kapiláry alebo pórov, kde kvapalina stúpa
- 1,5 - kontaktný uhol (θ)
- 2 Kapilárnosť vody
- 2.1 Na rastlinách
- 3 Odkazy
Charakteristiky kapilárnosti
-Povrch kvapaliny
Povrch kvapaliny, napríklad vody, v kapiláre je konkávny; meniskus je konkávny. Táto situácia nastáva preto, že výsledok síl pôsobiacich na molekuly vody v blízkosti steny trubice je nasmerovaný na toto.
Vo všetkých meniskách je kontaktný uhol (θ), čo je uhol, ktorý tvorí stenu kapilárnej trubice s čiarou dotýkajúcou sa povrchu kvapaliny v mieste dotyku..
Adhézne a kohézne sily
Ak prevláda adhézna sila kvapaliny ku kapilárnej stene nad medzimolekulovou kohéznou silou, potom je uhol θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
Keď sa kvapka vody umiestni na povrch čistého skla, voda sa šíri na sklo, takže θ = 0 a cos θ = 1.
Ak intermolekulová kohézna sila prevláda nad pevnosťou kapiláry pri adhézii na stene kvapaliny, napríklad v ortuti, meniskus bude konvexný a uhol 9 bude mať hodnotu> 90 °; ortuť nenavlhčuje kapilárnu stenu a preto prechádza cez vnútornú stenu.
Keď sa kvapka ortuti umiestni na povrch čistého skla, kvapka si zachováva svoj tvar a uhol θ = 140 °.
-výška
Voda stúpa cez kapilárnu trubicu, aby dosiahla výšku (h), v ktorej hmotnosť vodného stĺpca kompenzuje vertikálnu zložku medzimolekulovej kohéznej sily.
Ako stúpa viac vody, príde bod, kde gravitácia zastaví svoj vzostup, aj keď povrchové napätie pracuje vo váš prospech.
Keď sa to stane, molekuly nemôžu ďalej „stúpať“ po vnútorných stenách a všetky fyzické sily sa vyrovnávajú. Na jednej strane máte sily, ktoré podporujú vzostup vody, a na druhej strane vaša váha ju tlačí dole.
Jurinov zákon
Toto môže byť napísané matematicky nasledovne:
2 π rΥcosθ = ρgπr2hod
Tam, kde ľavá strana rovnice závisí od povrchového napätia, ktorého veľkosť súvisí aj s kohéznymi alebo intermolekulovými silami; Cos0 predstavuje kontaktný uhol a r polomer otvoru, ktorým kvapalina stúpa.
A na pravej strane rovnice máme výšku h, gravitačnú silu g a hustotu kvapaliny; to by bola voda.
Vymazanie potom máte
h = (2Υcosθ / ρgr)
Táto formulácia je známa ako Jurinov zákon, ktorý definuje výšku dosiahnutú kvapalinovým stĺpcom, v kapilárnej trubici, keď je hmotnosť kvapalinového stĺpca vyvážená silou vzostupu kapilárou..
-Povrchové napätie
Voda je dipolárna molekula, vďaka elektronegativite kyslíkového atómu a jeho molekulárnej geometrii. To spôsobuje, že časť molekuly vody, kde sa kyslík nachádza, je záporne nabitá, zatiaľ čo časť molekuly vody, ktorá obsahuje 2 atómy vodíka, je kladne nabitá.
Molekuly v kvapaline vďaka tomu pôsobia prostredníctvom viacerých vodíkových väzieb, ktoré ich držia pohromade. Molekuly vody, ktoré sú v rozhraní voda: vzduch (povrch), však podliehajú čistej príťažlivosti molekulami kvapalného sínusu, ktoré nie sú kompenzované slabou príťažlivosťou molekulami vzduchu..
Molekuly vody rozhrania sú preto vystavené atraktívnej sile, ktorá má tendenciu odstraňovať molekuly vody z rozhrania; to znamená, že vodíkové mostíky vytvorené s molekulami v spodnej časti ťahajú tie, ktoré sú na povrchu. Povrchové napätie sa teda snaží zmenšiť povrch rozhrania voda: vzduch.
Vzťah s h
Ak sa pozriete na rovnicu Jurinovho zákona, zistíte, že h je priamo úmerné Υ; čím väčšie je povrchové napätie kvapaliny, tým väčšia je výška, ktorá môže stúpať cez kapiláru alebo póry materiálu.
Dá sa teda očakávať, že pre dve kvapaliny A a B s rozdielnym povrchovým napätím stúpa ten, ktorý má najvyššie povrchové napätie..
Z tohto bodu možno vyvodiť, že najdôležitejšou charakteristikou, ktorá definuje kapilárnu vlastnosť kvapaliny, je vysoké povrchové napätie.
-Polomer kapiláry alebo pórov, kde stúpa kvapalina
Pozorovanie zákona Jurina naznačuje, že výška dosiahnutá kvapalinou v kapiláre alebo póroch je nepriamo úmerná polomeru tej istej kvapaliny..
Čím menší je teda polomer, tým väčšia je výška, ktorú dosiahne kvapalinový stĺpec kapilárnym pôsobením. To je možné vidieť priamo na obrázku, kde je voda porovnávaná s ortuťou.
V sklenenej trubici s polomerom 0,05 mm dosiahne vodný stĺpec kapilárnosťou výšku 30 cm. V kapilárnych trubiciach s polomerom 1 μm s podtlakom 1,5 x 103 hPa (ktorý sa rovná 1,5 atm) zodpovedá výpočtu výšky vodného stĺpca od 14 do 15 m.
To je veľmi podobné tomu, čo sa deje s tými slamkami, ktoré sa točia niekoľkokrát. Nasávaním kvapaliny vzniká tlakový rozdiel, ktorý spôsobuje, že kvapalina vstúpi do úst.
Maximálna hodnota výšky stĺpca dosiahnutého kapilárou je teoretická, pretože polomer kapilár nemožno znížiť nad určitú hranicu..
Zákon Poiseuille
To potvrdzuje, že tok skutočnej kvapaliny je daný týmto výrazom: \ t
Q = (πr4/ 8ηl) AP
Kde Q je prietok kvapaliny, η je jeho viskozita, 1 dĺžka trubice a AP rozdiel tlakov.
Keď sa zmenší polomer kapiláry, výška stĺpca kvapaliny dosiahnutá kapilárou by sa mala neobmedzene zvyšovať. Poiseuille však poukazuje na to, že zmenšenie polomeru tiež znižuje prietok kvapaliny cez túto kapiláru.
Okrem toho viskozita, ktorá je meradlom odporu, ktorý je proti prúdu skutočnej kvapaliny, by ďalej znižovala prietok kvapaliny..
-Uhol kontaktu (θ)
Čím vyššia je hodnota cos0, tým vyššia je výška vodného stĺpca kapilárnosťou, ako to naznačuje Jurinov zákon.
Ak je θ malé a blíži sa nule (0), cosθ je = 1, takže hodnota h bude maximálna. Naopak, ak je θ 90 °, cosθ = 0 a hodnota h = 0.
Keď je hodnota θ väčšia ako 90 °, čo je prípad konvexného menisku, kvapalina sa nezvyšuje kapilárou a jej tendencia je klesať (ako je to u ortuti)..
Kapilárnosť vody
Voda má hodnotu povrchového napätia 72,75 N / m, relatívne vysokú v porovnaní s hodnotami povrchového napätia nasledujúcich kvapalín:
-Acetón: 22,75 N / m
-Etylalkohol: 22,75 N / m
-Hexán: 18,43 N / m
-Metanol: 22,61 N / m.
Voda má preto výnimočné povrchové napätie, ktoré podporuje rozvoj kapilárneho javu, ktorý je potrebný pre absorpciu vody a živín rastlinami..
Na rastlinách

Kapilárnosť je dôležitým mechanizmom pre vznik miazgy xylémom rastlín, ale sama o sebe nie je dostatočná na to, aby sa miazga dostala do listov stromov..
Transpirácia alebo odparovanie je dôležitým mechanizmom vo vzostupe miazgy xylémom rastlín. Listy strácajú vodu odparovaním, čo vedie k poklesu množstva molekúl vody, čo spôsobuje príťažlivosť molekúl vody prítomných v kapilárnych trubiciach (xylém).
Molekuly vody nekonajú nezávisle od seba, ale interagujú Van der Waalsovými silami, čo spôsobuje, že sa stúpajú spojené kapilárnymi trubicami rastlín smerom k listom..
Okrem týchto mechanizmov treba poznamenať, že rastliny absorbujú vodu z pôdy osmózou a že pozitívny tlak vyvolaný v koreňoch poháňa začiatok výstupu vody cez kapiláry rastliny..
referencie
- García Franco A. (2010). Povrchné javy. Zdroj: sc.ehu.es
- Povrchové javy: povrchové napätie a kapilárnosť. [PDF]. Zdroj: ugr.es
- Wikipedia. (2018). Kapilarita. Zdroj: en.wikipedia.org
- Risvhan T. (s.f.) Kapilárnosť v rastlinách. Zdroj: academia.edu
- Helmenstine, Anne Marie, Ph.D. (22. decembra 2018). Kapilárne pôsobenie: Definícia a príklady. Zdroj: thinkco.com
- Ellen Ellis M. (2018). Kapilárne pôsobenie vody: Definícia a príklady. Štúdia. Zdroj: study.com
- Personál ScienceStruck. (16. júl 2017). Príklady, ktoré vysvetľujú koncepciu a význam kapilárnej akcie. Zdroj: sciencestruck.com


