Kolínový systém a príklady
lineárne vektory Sú jedným z troch typov existujúcich vektorov. Ide o tie vektory, ktoré sú v rovnakom smere alebo línii pôsobenia. To znamená nasledovné: dva alebo viac vektorov budú kolineárne, ak sú usporiadané v priamkach, ktoré sú navzájom rovnobežné.
Vektor je definovaný ako množstvo aplikované na telo a charakterizované ako smer, zmysel a mierka. Vektory sa môžu nachádzať v rovine alebo v priestore a môžu byť rôznych typov: súradnicové vektory, súbežné vektory a paralelné vektory.

index
- 1 colineal vektorov
- 2 Charakteristiky
- 2.1 Príklad 1
- 2.2 Príklad 2
- 2.3 Príklad 1
- 3 Kolínový vektorový systém
- 3.1 Kolineárne vektory s opačnými zmyslami
- 3.2 Kollinické vektory s rovnakým významom
- 3.3 Kolineárne vektory s rovnakými veličinami a opačnými zmyslami
- 4 Rozdiel medzi lineárnymi a súbežnými vektormi
- 5 Referencie
Collinear vektory
Vektory sú kolineárne, ak línia pôsobenia jedného z nich je presne rovnaká línia pôsobenia všetkých ostatných vektorov, bez ohľadu na veľkosť a zmysel každého z vektorov..
Vektory sa používajú ako reprezentácie v rôznych oblastiach, ako je matematika, fyzika, algebra a tiež v geometrii, kde sú vektory kolineárne len vtedy, keď je ich smer rovnaký, bez ohľadu na to, či ich význam nie je.
rysy
- Dva alebo viac vektorov sú kolineárne, ak je vzťah medzi súradnicami rovnaký.
Príklad 1
Máme vektory m = m_x; m_y a n = n_x; n_y. Tieto sú kolineárne, ak:
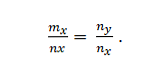
Príklad 2
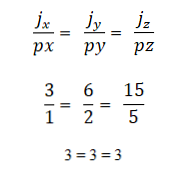
- Dva alebo viac vektorov sú kolineárne, ak sa násobenie produktu alebo vektora rovná nule (0). Je to preto, že v súradnicovom systéme je každý vektor charakterizovaný svojimi príslušnými súradnicami, a ak sú navzájom úmerné, vektory budú kolineárne. Vyjadruje sa takto:
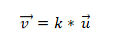
Príklad 1
Máme vektory a = (10, 5) a b = (6, 3). Na určenie, či sú kolineárne, sa používa teória determinantov, ktorá stanovuje rovnosť krížových produktov. Týmto spôsobom musíte:
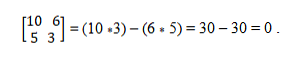
Kolínový vektorový systém
Kolineárne vektory sú znázornené graficky pomocou smeru a zmyslu týchto - uvažujúcich, že musia prejsť bodom aplikácie - a modulom, ktorý je určitým rozsahom alebo dĺžkou..
Systém kolineárnych vektorov sa vytvára vtedy, keď dva alebo viac vektorov pôsobí na objekt alebo telo, ktoré predstavujú silu a pôsobia v rovnakom smere..
Napríklad, ak sú na teleso aplikované dve kolineárne sily, výsledok týchto bude závisieť len od smeru, v ktorom pôsobia. Existujú tri prípady, ktorými sú:
Kolineárne vektory s opačnými zmyslami
Výsledok dvoch kolineárnych vektorov sa rovná súčtu týchto hodnôt:
R = = F = F1 + F2.
príklad
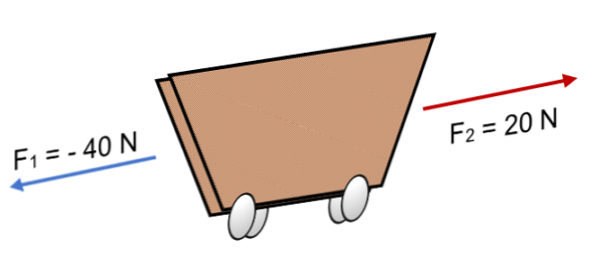
Ak dve sily pôsobia na vozík F1 = 40 N a F2 = 20 N v opačnom smere (ako je znázornené na obrázku), výsledkom je:
R = F = (- 40 N) + 20N.
R = -20 N.
Kollinárne vektory s rovnakým významom
Veľkosť výslednej sily sa bude rovnať súčtu kolineárnych vektorov:
R = = F = F1 + F2.
príklad
Ak dve sily pôsobia na vozík F1 = 35 N a F2 = 55 N v rovnakom smere (ako je znázornené na obrázku), výsledkom je:
R = = F = 35N + 55N.
R = 90 N.
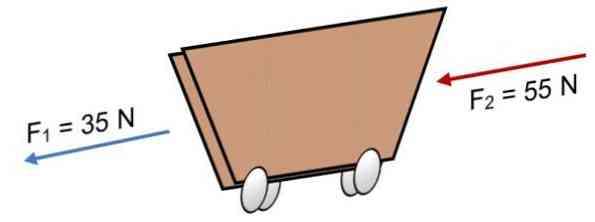
Pozitívny výsledok ukazuje, že kolineárne vektory pôsobia vľavo.
Kollinárne vektory s rovnakými veličinami a opačnými zmyslami
Výsledok dvoch kolineárnych vektorov bude rovný súčtu kolineárnych vektorov:
R = = F = F1 + F2.
Keďže sily majú rovnakú veľkosť, ale v opačnom smere - to znamená, že jedna bude pozitívna a druhá záporná - pri pridaní dvoch síl sa výsledná hodnota rovná nule..
príklad
Ak dve sily pôsobia na vozík F1 = -7 N a F2 = 7 N, ktoré majú rovnakú veľkosť, ale v opačnom smere (ako je znázornené na obrázku), výsledkom je:
R = F = (-7N) + 7N.
R = 0.
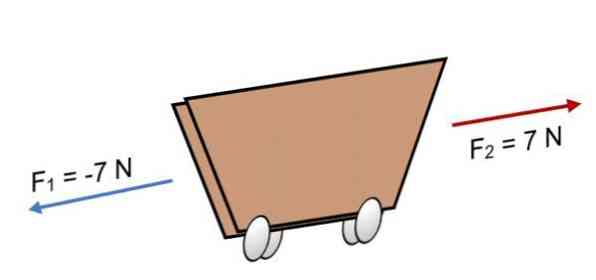
Keďže výsledná hodnota sa rovná 0, znamená to, že vektory sú navzájom vyvážené, a preto je telo v rovnováhe alebo v pokoji (nebude sa pohybovať).
Rozdiel medzi lineárnymi a súbežnými vektormi
Kollinárne vektory sú charakterizované tým, že majú rovnaký smer na tej istej čiare, alebo preto, že sú rovnobežné s priamkou; to znamená, že sú vektormi priame paralelné línie.
Na druhej strane sú súbežné vektory definované, pretože sú v rôznych riadkoch pôsobenia, ktoré sú zachytené v jednom bode.
Inými slovami, majú rovnaký východiskový bod alebo miesto príchodu - bez ohľadu na ich modul, smer alebo smer - a vytvárajú medzi nimi uhol.
Systémy súbežných vektorov sú riešené matematickými metódami alebo grafmi, ktoré sú metódou paralelogramu síl a metódy mnohouholníka síl. Prostredníctvom týchto hodnôt bude určená hodnota výsledného vektora, ktorá označuje smer, ktorým sa bude telo pohybovať.
V podstate je hlavným rozdielom medzi kolinárnymi vektormi a súbežnými vektormi línia pôsobenia, v ktorej pôsobia: kolineárne pôsobia v rovnakom riadku, zatiaľ čo súčasné v rôznych.
To znamená, že kolineárne vektory pôsobia v jednej rovine, "X" alebo "Y"; a súbežné pôsobenie v oboch rovinách, počnúc od toho istého bodu.
Kolineárne vektory nie sú v bode, rovnako ako súbežné, pretože sú navzájom paralelné.
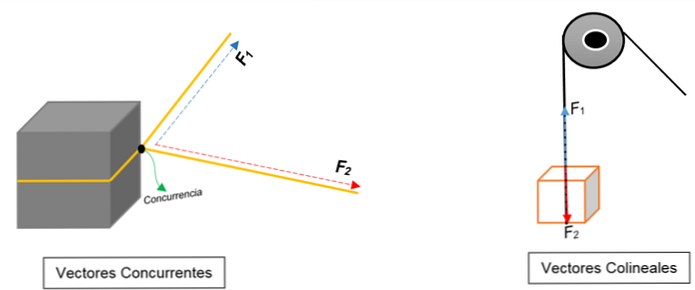
V ľavom obrázku môžete vidieť blok. Je zviazaný lanom a uzol ho delí na dva; keď sa ťahá smerom k rôznym orientáciám as rôznymi silami, blok sa bude pohybovať v rovnakom smere.
Dva vektory sú znázornené tak, že sa zhodujú v bode (blok), bez ohľadu na ich modul, zmysel alebo smer.
Namiesto toho sa v pravom obrázku objaví kladka, ktorá zdvíha box. Lano predstavuje líniu činnosti; keď je ťahaná, pôsobia na ňu dve sily (vektory): jedna sila napätia (pri šplhaní na blok) a iná sila, tá, ktorá vyvíja hmotnosť bloku. Obidva majú rovnaký smer, ale v opačných smeroch; sa nezhodujú v bode.
referencie
- Estalella, J. J. (1988). Vektorová analýza. Zväzok 1.
- Gupta, A. (s.f.). Vzdelávanie Tata McGraw-Hill.
- Jin Ho Kwak, S. H. (2015). Lineárna algebra. Springer Science & Business Media.
- Montiel, H. P. (2000). Fyzika 1 pre technologickú maturitu. Redakčná skupina Patria.
- Santiago Burbano de Ercilla, C. G. (2003). Všeobecná fyzika Redakčný Tebar.
- Sinha, K. (s.f.). Textová kniha matematiky XII. 2. Rastogiho publikácie.


