Koľko osí symetrie má kruh?
symetrické osi kruhu Sú nekonečné. Tieto osi sú tie, ktoré rozdeľujú geometrický tvar do dvoch presne rovnakých polovíc.
Kruh sa skladá zo všetkých bodov, ktorých vzdialenosť k pevnému bodu je menšia alebo rovná určitej hodnote "r"..
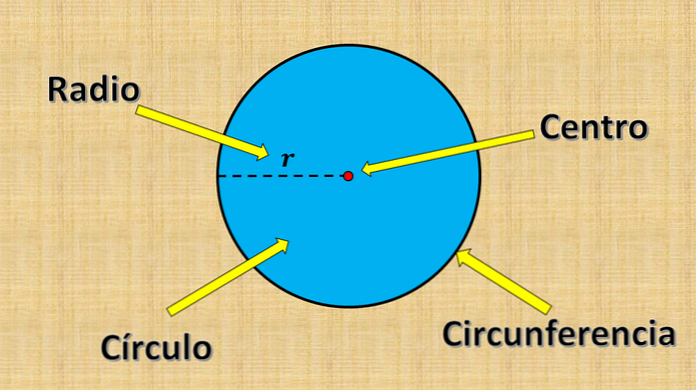
Vyššie uvedený pevný bod sa nazýva stred a hodnota "r" sa nazýva polomer. Polomer je najväčšia vzdialenosť medzi bodom kruhu a stredom.
Na druhej strane, akýkoľvek segment čiary, ktorého konce sú na okraji kruhu (obvod) a prechádza stredom, sa nazýva priemer. Jeho meranie sa vždy rovná dvojnásobku polomeru.
Kruh a obvod
Nezamieňajte kruh s kruhom. Obvod sa týka len bodov, ktoré sú vo vzdialenosti "r" od stredu; to znamená iba okraj kruhu.
Pri hľadaní osí symetrie je však ľahostajné, ak pracujete s kruhom alebo s kruhom.
Čo je os symetrie?
Os symetrie je čiara, ktorá delí na dve rovnaké časti určitý geometrický obrazec. Inými slovami, os symetrie pôsobí ako zrkadlo.
Hriadele symetrie kruhu
Ak pozorujete akýkoľvek kruh, bez ohľadu na jeho polomer, môžete vidieť, že nie každý riadok, ktorý prechádza, je osou symetrie.
Napríklad žiadna z čiar nakreslených v nasledujúcom obrázku nie je osou symetrie.
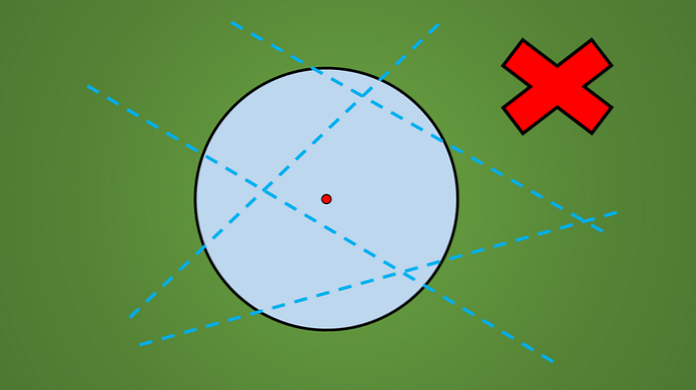
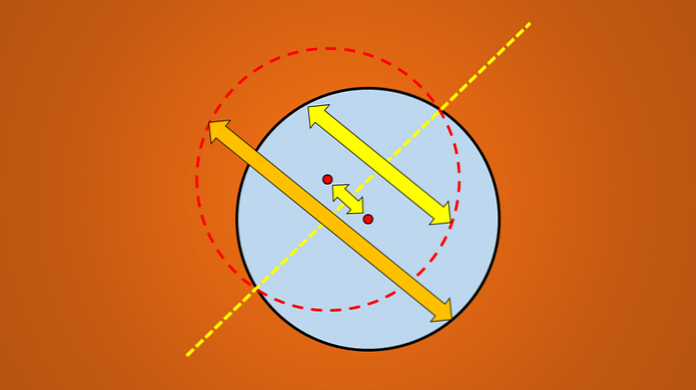
Jednoduchý spôsob, ako skontrolovať, či čiara je osou symetrie alebo nie, je odrážať kolmo geometrický obrazec na opačnú stranu čiary.
Ak odraz nezodpovedá pôvodnému obrázku, táto čiara nie je osou symetrie. Nasledujúci obrázok ilustruje túto techniku.
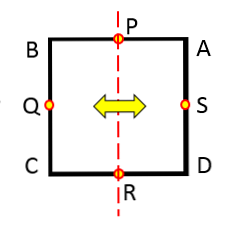
Ak je však uvažovaný nasledujúci obraz, je dobre známe, že nakreslená čiara je osou symetrie kruhu.
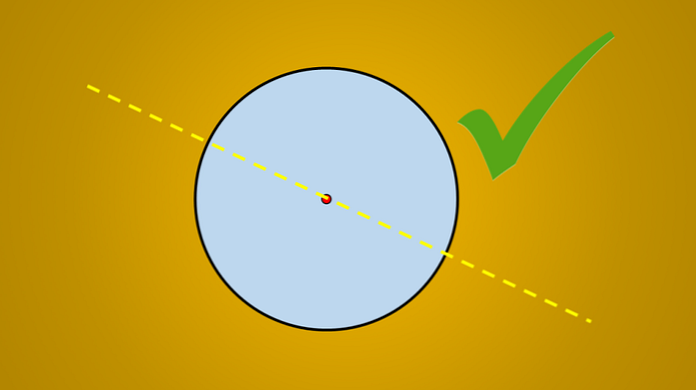
Otázkou je, či existuje viac osí symetrie? Odpoveď znie áno. Ak túto čiaru otočíte o 45 ° proti smeru hodinových ručičiek, získaná čiara je tiež osou symetrie kruhu.
To isté sa stane, ak otočíte o 90 °, 30 °, 8 ° a vo všeobecnosti o ľubovoľný počet stupňov.
Dôležité na týchto riadkoch nie je sklon, ktorý majú, ale všetci prechádzajú stredom kruhu. Preto každá čiara, ktorá obsahuje priemer kruhu, je osou symetrie.
Keďže kruh má nekonečný počet priemerov, potom má nekonečný počet osí symetrie.
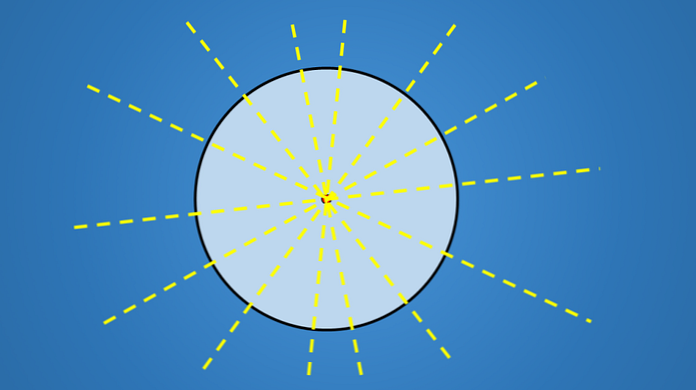
Ostatné geometrické obrazce, ako napríklad trojuholník, štvoruholník, päťuholník, šesťuholník alebo akýkoľvek iný mnohouholník, majú konečný počet osí symetrie.
Dôvod, prečo má kruh nekonečný počet osí symetrie je, že nemá žiadne strany.
referencie
- Basto, J. R. (2014). Matematika 3: Základná analytická geometria. Redakčná skupina Patria.
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: prístup k riešeniu problémov učiteľov základných škôl. López Mateos Editori.
- Bult, B., & Hobbs, D. (2001). Matematický slovník (znázornené na obr.). (F. P. Cadena, Trad.) Edícia AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometria. Reforma horného cyklu E.G.B. Ministerstvo školstva.
- Schneider, W., & Sappert, D. (1990). Praktický technický nákres: úvod do základov priemyselnej technickej kresby. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Výpočet: niekoľko premenných. Pearson Education.


